Complex Limits to Infinity

By now, we've established the concept of a limit when working with a complex space. It turns out that it's basically the exact analogue of the real definition of a limit, which, if you'll recall, is

$\forall \epsilon,\ \exists \delta\ s.t.\ 0 \lt |x - c| \lt \delta \to |f(x) - L| \lt \epsilon$

In complex space, we have a similar concept - we replace the absolute value bars with the modulus (which are, in effect, the same thing anyway).

$\forall \epsilon,\ \exists \delta\ s.t.\ |z - z_0| \lt \delta \to |f(z) - w_0| \lt \epsilon$

We use this definition in a similar way. But how about limits to infinity?

In single variable calculus, we said that, for whichever "direction" of infinity we're choosing to travel in ($-\infty$ or $\infty$). we can choose an arbitrarily large (or small) number beyond which the function will approach some limit $L$. More formally,

$\forall \epsilon,\ \exists N\ s.t.\ x \gt N \to |f(x) - L| \lt \epsilon$

But what does it even mean to travel in a "direction" of infinity on the complex plane? Aren't there a million paths? What does it mean to be inside some $B_\delta(\infty)$?

First, we'll take a tangent into the world of stereographic projections. Take a circle, cut in half by the real number line. We can draw a line through the top of the circle and every single point ($P$') on the real number line, which will intersect another point on the circle itself ($P$).

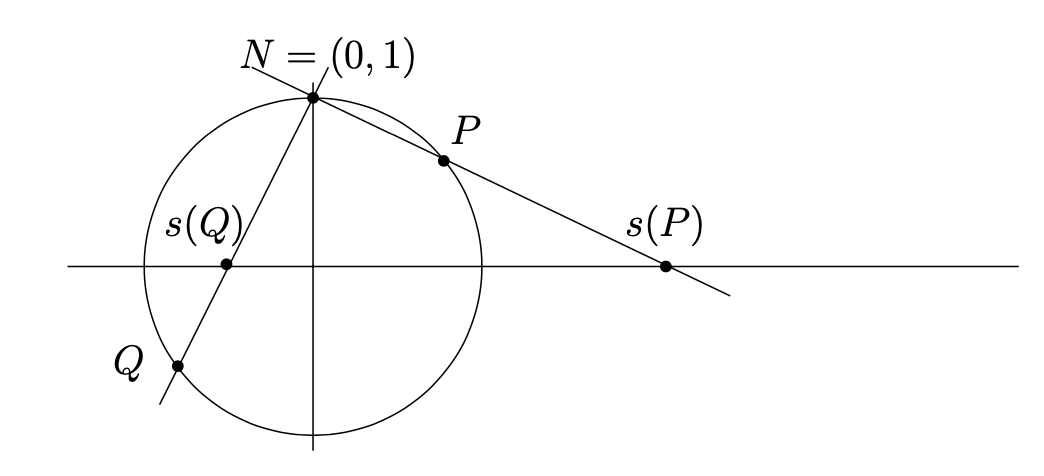(image credits to Wikipedia).

We've effectively created a map of the real number line onto this one circle. Furthermore, you'll notice that, as we near infinity, our mapped point nears the very top of the circle, where all of our rays originate from: $N$.

Now, extend this to the complex plane (two dimensions). Instead of a circle, we have a sphere, with an intersecting equatorial plane. We similarly draw lines from the top of our circle, mapping points on the actual complex plane to points on the sphere.

(again, credits to Wikipedia).

This is called the Riemann sphere. What this projection does is it realizes this abstract concept of $\infty$ into a "physical" point that we can grapple with. Any $\delta$-neighborhood around $\infty$ can just be visualized as a neighborhood drawn on the top of the sphere, which can then be mapped onto boundaries on the complex plane.

More formally, we define an $\epsilon$-neighborhood of $\infty$ to be the set of points

${z \in \mathbb{C}\ |\ |z| \gt \frac{1}{\epsilon}}$

Why $\frac{1}{\epsilon}$, you ask? We could choose any arbitrarily large number, like $N$ in our example with real, single variable functions. However, $\frac{1}{\epsilon}$ makes it extra clear that, with some small number $\epsilon$, we use its large reciprocal (it also makes the coming proofs just a bit nicer).

With this definition, we can formulate a statement of limits:

$\forall \epsilon\ \exists \delta\ s.t.\ |z| \gt \frac{1}{\delta} \to |f(z) - w_0| \lt \epsilon$

means

$\lim_{z \to \infty} f(z) = w_0$

Meanwhile,

$\forall \epsilon\ \exists \delta\ s.t.\ 0 \lt |z - z_0| \lt \delta \to |f(z)| \gt \frac{1}{\epsilon}$

means

$\lim_{z \to z_0} f(z) = \infty$

We can derive some pretty cool properties that can help us evaluate certain limits to infinity.

Case 1

$\lim_{z \to z_0} f(z) = \infty \Longleftrightarrow \lim_{z \to z_0} \frac{1}{f(z)} = 0$

We first assume the statement $\lim_{z \to z_0} f(z) = \infty$, which tells us

$|z - z_0| \lt \delta \to |f(z)| \gt \frac{1}{\epsilon}$

by definition. We can then reciprocate:

$|\frac{1}{|f(z)} - 0| \lt \epsilon,\ |z - z_0| \lt \delta$

which yields

$\lim_{z \to z_0} \frac{1}{f(z)} = 0$

Case 2

$\lim_{z \to \infty} f(z) = w_0 \Longleftrightarrow \lim_{z \to 0} f\left(\frac{1}{z}\right) = w_0$

Once again, we assume $\lim_{z \to \infty} f(z) = w_0$. By definition, then,

$|z| \gt \frac{1}{\delta} \to |f(z) - w_0| \lt \epsilon$

Manipulating the left side,

$|\frac{1}{z}| \lt \delta \to |f(z) - w_0| \lt \epsilon$

We can "choose" $z = \frac{1}{z}$. (If this feels weird to you, remember that we can choose some auxiliary variable $a = \frac{1}{z}$, and then "rename" $a$ to $z$ in the formal limit statement, which is why we're allowed to do this next part). Plugging in $\frac{1}{z}$ for $z$, we get

$|z| \lt \delta \to |f\left(\frac{1}{z}\right) - w_0| \lt \epsilon$

By definition, this becomes the limit

$\lim_{z \to 0} f\left(\frac{1}{z}\right) = w_0$

Case 3

$\lim_{z \to \infty} f(z) = \infty \Longleftrightarrow \lim_{z \to 0} \frac{1}{f(1/z)} = 0$

To see why this is true, we first assume the left side of the statement (sound familiar?). From $\lim_{z \to \infty} f(z) = \infty$, we get, by definition,

$|z| \gt \frac{1}{\delta} \to |f(z)| \gt \frac{1}{\epsilon}$

This time, we can reciprocate for both statements, yielding

$|\frac{1}{z}| \lt \delta \to |\frac{1}{f(z)}| \lt \epsilon$

Revisiting our trick from case 2, we can "choose" $z = \frac{1}{z}$ and get

$|z| \lt \delta \to |\frac{1}{f(1/z)}| \lt \epsilon$

which is the formal statement of the limit

$\lim_{z \to 0} \frac{1}{f(1/z)} = 0$